Multiplication of 2-Digit Numbers

At the completion of this unit, students will be able to multiply 2-digit numbers using arrays. Arrays are a conceptual way of solving a problem as they are able to use the procedures used from finding place value to solve an algorithm. Students have already learned to use arrays and to find the product of 2-digit integers but only with numbers that are multiples of ten. This unit will strengthen and increase their understanding of the procedures of solving multiplication equations by developing concepts further.
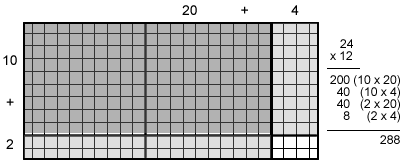
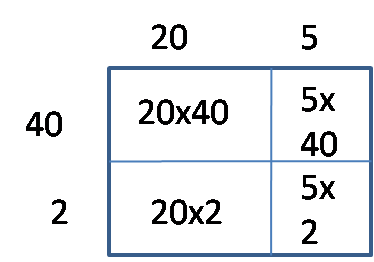
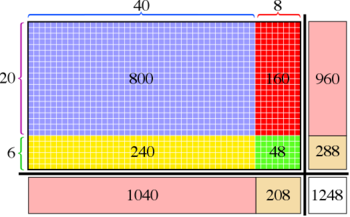
Earlier in the year, students solidified their skills of solving products of one-digit numbers. Arrays allow students to use images and the distributive property to break complex problems into simpler ones. Students will be able to break down factors by place value using areas of rectangles to represent partial products. They will also use 2x2 tables placing a number in each box and outside the boxes to break apart a problem into problems that are easier to manage for students. With both arrays and tables, students are able to focus on the place values and the partial products to increase their understanding of multiplication concepts. Students will write out the partial products into expanded algorithms in order to use what they know about basic one digit multiplication and 2-digit multiplication of multiples of ten.
As students continue to practice and develop their understanding of finding products, they will be able to become more fluent with problem solving. Throughout the year we have developed students fluency of solving one digit multiplication problems. We are now introducing more complex problems by breaking down the parts into pieces they have more fluency with. As Bornemann, Bright et. al. state “Fluency with algorithms sets the stage for more sophisticated understanding of mathematics ideas” (P. 1).
Earlier in the year, students solidified their skills of solving products of one-digit numbers. Arrays allow students to use images and the distributive property to break complex problems into simpler ones. Students will be able to break down factors by place value using areas of rectangles to represent partial products. They will also use 2x2 tables placing a number in each box and outside the boxes to break apart a problem into problems that are easier to manage for students. With both arrays and tables, students are able to focus on the place values and the partial products to increase their understanding of multiplication concepts. Students will write out the partial products into expanded algorithms in order to use what they know about basic one digit multiplication and 2-digit multiplication of multiples of ten.
As students continue to practice and develop their understanding of finding products, they will be able to become more fluent with problem solving. Throughout the year we have developed students fluency of solving one digit multiplication problems. We are now introducing more complex problems by breaking down the parts into pieces they have more fluency with. As Bornemann, Bright et. al. state “Fluency with algorithms sets the stage for more sophisticated understanding of mathematics ideas” (P. 1).